W1292 Useful Randomness

Within these castle walls be forged Mavens of Computer Science ...

— Merlin, The Coder

Random Bitmap

Kuntze-Konicz Fortune

Prerequisites

• W1151 Conditional and Flow Chart
• W1152 While Loop
• W1153 Repeat-While Loop
• W1154 For Loop

Research

• [1](wikipedia)-Pythagorean's Theorem
• Random Number Generation (Wikipedia)
• How Random is Your Randomness?
• The Search for π
• Random Function for Int (Swift Documentation)
• Random Function for Double (Swift Documentation)

Introduction

In Swift, it is possible to return random numbers within a range as a method. Using .random allows you to choose a number within a range. The for loop below demonstrates a range of numbers and random numbers printed each time the loop runs. Here, we demonstrate the randomness applied to an Int.

Int

for _ in 1...5 {
    print(Int.random(in: 1..<50))
}
// Prints "49"
// Prints "32"
// Prints "15"
// Prints "9"

As you can see, .random is highlighted in the correct location of where it should be applied.

The Double

In Swift .random can also be applied to Doubles just like Int, as shown above. It is the same idea, but with a double instead of Int and a different output.

for _ in 1...5 {
    print(Double.random(in: 1..<50))
}
// Prints "49.0"
// Prints "32.0"
// Prints "15.0"
// Prints "9.0"

Pythagorean theory

This is Pythagorean's Theorem

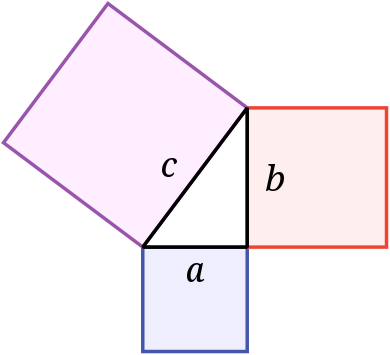
Pythagorean's theorem is an important concept in Euclidean geometry regarding the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle), also known as c, is equal to the sum of the areas of the squares on the other two sides. The other two sides are known as a and b, a being the adjacent and b being the opposite. This theorem is often written as a + b = c.

Trigonometric ratios

Trigonometric ratios

Sin and Cos are both concepts of geometry that tie into Pythagorean's Theorem. Soh-Cah-Toa is an acronym used to remember the formulas to solve simple sin and cos functions, Toa known as tangent is explained later. Focus on sin and cos for now. Before moving on, recollect the names of each triangle side that was described earlier in the Pythagorean's Theorem.

Sine(Sin)

• Soh is Sin = opposite (b) / hypotenuse (c)

Cosine(Cos)

• Cah is Cos = adjacent (a) / hypotenuse (c)

Tangent(Toa)

• Toa is Tan = opposite (b) / adjacent (a)

Applications in Swift

In Swift, you can apply Sine, Cosine, and Tangent in different ways. In this example, we start by importing a library. This allows us to apply the prebuilt math formulas, thus the import Foundation. If you are not familiar with Swift's libraries, it is okay. We will cover this in another lesson.

import Foundation 
//importing the library, allows us to use the sin, cos, and tan functions 
//Double.pi is a Double since pi has decimals 

let sine = sin(90 * Double.pi / 180)
print("Sine \(sine)")

let cosine = cos(90 * Double.pi / 180)
print("Cosine \(cosine)")

let tangent = tan(90 * Double.pi / 180)
print("Tangent \(tangent)")

//Output:
//Sine 1.0
//Cosine 6.12323399573677e-17
//Tangent 1.63312393531954e+16

Excursions

If you would like to experiment, that is great!

• Start by opening the swift REPL by typing in Swift as shown below.

john-williams@codermerlin:~$  swift

• Proceed to import Foundation.

john-williams@codermerlin:~$  import Foundation

• Finally, to have the best learning experience, explore this concept on your own.
• You can reference the for loop example and experiment; try changing the line value to have different results.
• Always remember to have fun!

Background

	Coming Soon
	Add section on throwing dart at ¼ of square

The value of π can be calculated by:

1. Randomly throwing "darts" at a unit circle
2. Counting the total number of "darts", N
3. Counting the number of "darts" that fall within the unit circle, C
4. The ratio of the area inside the circle to the total area is C / N
5. The value of π is four times this value (because the area of the total square is 2 units x 2 units)

Prepare

Create a new directory in your ~/Experiences directory named "W1292". Use emacs to edit a file named "main.swift":

zay-vin@codermerlin:~$  cd ~/Experiences

zay-vin@codermerlin:~/Experiences$  mkdir W1292

zay-vin@codermerlin:~/Experiences$  cd W1292

zay-vin@codermerlin:~/Experiences/project-1292$  swift-init

zay-vin@codermerlin:~/Experiences/project-1292$  emacs main.swift

Helpful Hint

You can run your program from within emacs with F5-r

Helpful Hint

You can find the square root of a number using the squareRoot function. This function is included in the Foundation library, so it must be imported.

For example:

import Foundation

let d = 12.0
print(d.squareRoot())

Observe

Observe, Ponder, and Journal: Section 1

Complete your program, then answer these questions:

1. Estimate the value of π using your program
   1. Throw 100 darts (N = 100). What result do you obtain?
   2. Throw 1000 darts (N = 1000). What result do you obtain?
2. How is the second result different from your previous result?
3. How large should N be to accurately estimate π to five digits?
4. How important is it that the dart be "thrown" randomly?

Exercises

Exercises

• Write a program that randomly throws a series of N darts at a virtual dartboard as described above. At the conclusion of throwing N darts, the program should print an estimate for the value of $\pi$. Be sure to complete this part of the exercise in your ~/Experiences/W1292 directory.
•  J1292  Create a journal and answer all questions in this experience. Be sure to include all sections of the journal, properly formatted.
•  M1292-28  Complete  Merlin Mission Manager  Mission M1292-28.

Key Concepts

Key Concepts

• Random numbers meet the following two criteria:
  • Even distribution over a defined interval
  • Impossible to predict subsequent values based on previous values
• Random numbers can be very useful in certain circumstances

CoderMerlin™ proudly recommends:

Your purchase via these links helps keep  Coder Merlin™ 's orbuculum ablaze. As an Amazon Associate we earn from qualifying purchases. Thank you for your support!