W2211 Stack
Prerequisites[edit]
Introduction[edit]
In Computer Science, the Stack is a very specific form of Linear Data Structure.[1] We've looked at Linear Data Structures already with those such as Arrays and Linked Lists. A Stack, however, is special because it's a structure where the order of the data dictates its use case. In this experience, we'll take a look at the Stack's conceptual structure, when it's used, and how to implement it.
Structure[edit]
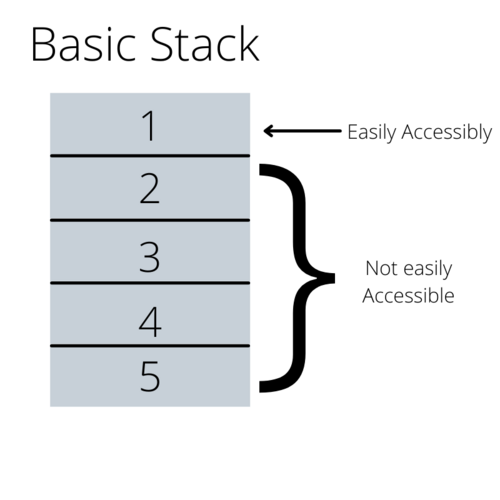
The best way to understand a Stack is visually. Simply imagine a physical stack of anything, textbooks for instance. In most cases, you can see only the top book in a stack. Furthermore, you cannot easily access any of the entries in the stack except for the top book. These are the two characteristics that define the Stack data structure. You can see and interact with only the top-most entry.[2]
These characteristics limit the Stack to about three different methods: push(), pop(), and peek().[2]
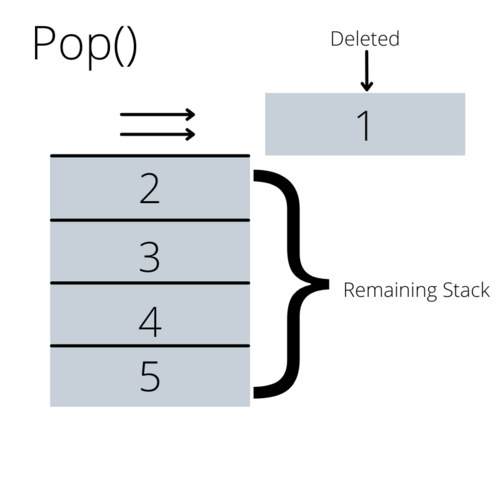
The pop() method simply removes the top-most entry on a stack, like sliding the top book off of the stack of books. It is much like a remove method.
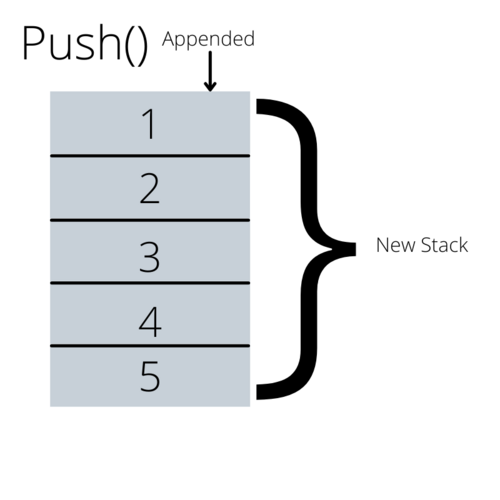
The push() method pushes another item to the top of the stack, like putting another book on top of a stack of books. It is much like an append method for similar structures.
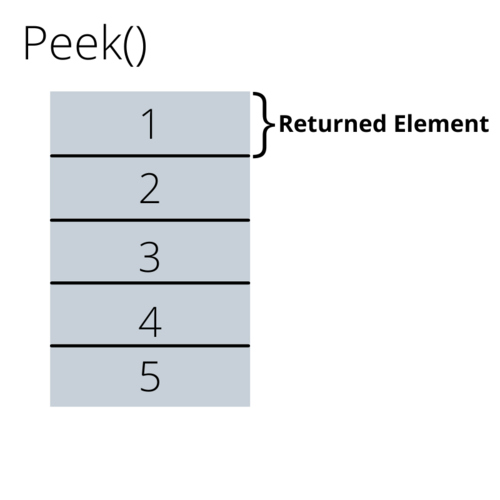
Finally the peek() method allows you to look at the top-most entry of the stack, much like a get method but limited to only one entry.
Keep in mind, this functionality is limited deliberately to reflect certain scenarios that are algorithmically the same. In fact, these characteristics put the Stack into a common pattern known as LIFO,[3] which stands for Last-In, First-Out. That is to say, the last entry put onto a stack is the first one taken out because the pop method can only remove the element that was last pushed on. (This pattern can also be referred to as FILO: First-In, Last-Out).
Quiz[edit]
Usage[edit]
At this point, you might be wondering why you would use such a limited data structure when arrays or linked lists provide more flexibility. A common pattern you'll notice in Computer Science is that more flexibility is not necessarily ideal. The Stack forces certain functions and programs to follow the LIFO pattern, and this pattern can be seen all over.
Think of an Undo button, for instance. It can be implemented by using the Stack because the purpose of the undo and redo buttons is popping off and pushing on the most recent edits, the exact LIFO pattern.[4] If this were implemented using an Array, it's more likely that an error could occur with restoring the wrong edits.
Stacks can also be used to manage recursive functions.[4] The most recent call to a recursive function would be pushed onto a stack and popped off when it has been resolved. This is why infinite recursion leads to the StackOverflow Error. But imagine if this functionality was made using a more flexible data structure, the program could accidentally diverge from the desired pattern if the code is not written in high quality. However, a Stack ensures that only the LIFO pattern is followed.
For this reason, Stacks are used in any scenario where the LIFO pattern needs to be simulated such as with recursion, undo buttons, caching, etc.
Quiz[edit]
Swift Implementation[edit]
You can implement the Stack in a few different ways. Next, we'll implement the structure using both an array and nodes that resemble more of a Singly Linked List (remember that stacks are a common usage for linked lists).
Let's start by using arrays, a simpler approach. For this, we'll use Generic typing. We will first make a struct called Stack that has exactly one variable called array. In this array, we'll have the Generic type T and keep it empty for now.
struct Stack<T>{
public var array: [T] = []
}
Next, we have to do implement the three methods: Push, Pop, and Peek. Thankfully, Swift has built-in properties and methods in the Array Class. So this process very easy. For the Push method, we can simply take in a variable called element of type T and append the element to the end of the array.
For the pop method, Swift has a handy function called poplast() built into the arrays. This function mimics the exact use case of our pop function. Finally, every array has the property "last", which returns the last element in the array. We can use this for our peek method by returning array.last. Note that we'll want pop and peek to be able to return nil if the Stack is empty.
mutating func push(_ element: T){
array.append(element)
}
mutating func pop()->T?{
return array.popLast()
}
func peek()->T?{
return array.last
}
Essentially everything that's all we need for a Stack implemented through the array. For convenience to more easily visualize the Stack, we'll use a CustomStringConvertible courtesy of raywenderlich.com.[2]
extension Stack: CustomStringConvertible {
var description: String {
let topDivider = "---Stack---\n"
let bottomDivider = "\n-----------\n"
let stackElements = array.map { "\($0)" }.reversed().joined(separator: "\n")
return topDivider + stackElements + bottomDivider
}
}
You can now test the stack by using the pop, push, and peek methods and then print out the whole stack for visualization. The following is an example.
var books = Stack<String>()
books.push("Eye of The World")
books.push("Final Empire")
books.push("Oathbringer")
books.push("First Law")
books.push("The Lightning Thief")
Now, let's try to make a Stack using Nodes. This is more complicated because we need to make a Node class and a Stack class. Let's get started by making the Node. This will be a typical Node with the features discussed in the W2294 Singly-Linked Lists article.
class Node<T> {
var value:T
var next:Node?
init(value:T) {
self.value = value
}
}
Now we need to make a class for the Stack. Because, in a stack, we care only about the top-most element, we'll have only one variable called head. We can very easily implement the peek() method by returning the head.
class NodeStack<T> {
var head:Node<T>?
func peek () -> Node<T>? {
return head
}
}
The Pop() and Push() methods are a little more tricky because we have to manipulate the Node's pointers. For the push method, we take in an input, much in the same way as we did for the arrays. Then we'll create a node using that value. Now, we'll use a simple if statement. If the head is nil (meaning the stack is empty), we set our head to the new node we created.
At this point, it's important to recall from the Singly Linked Lists article that Nodes with only one pointer can travel in only one direction. Your intuition might tell you to have the pointers move toward the node that has been put in last but a more practical implementation would be to have the points moving toward the node that was pushed first because that's the way the head would be traveling.
So, if the stack is not empty, we handle this by creating a constant called headNode. This will be the node of the head before we change the head to our new node. We'll set our new node's next to be the old head (headNode) and then set the Stack's head variable to be our new node.
func push(_ value:T){
let node = Node<T>(value: value) //create node with given value
if (head == nil) { //check if stack is empty
head = node
}
else {
let headNode = head //store old head in headNode
node.next = headNode
head = node //set head to our new node
}
}
Now, for the pop method, we do mostly the same thing. First, we check if the Stack is empty. If it is, we return nil. Otherwise, we create two constants, each representing the current head. We'll set our head variable to headNode.next, essentially making the head be represented by the next entry down the stack. Then we set our node variable's next to be nil, essentially breaking its pointer away from the rest of the stack and deleting it. Finally, we return the node we had just deleted.
func pop() -> Node<T>? {
if (head == nil) {
return nil
}
let headNode = head //set headNode to the current head
let node = headNode //create constant node to current head
head = headNode!.next //set our new head to the old head's next, going down the stack
node!.next = nil //break node's pointer away from the stack thus deleting it
return node
}
And just like that, we have all three functions that are needed to create a stack using nodes. As an exercise, try thinking of how you can add some useful properties onto the NodeStack class such as isEmpty() and size().
Key Concepts[edit]
- Stacks are a Linear Data Structure with several purposeful limitations.
- Stacks are meant to be used to represent the LIFO pattern where the last entry put in is the first entry out.
- Stacks have three main functions: push() appends an item to the top, pop() removes the item at the top, and peek() returns the item at the top.
- Stacks are used in several applications such as for undo buttons, recursion management, and caching.