Number Systems

Within these castle walls be forged Mavens of Computer Science ...

— Merlin, The Coder

Positional Notation

Positional notation (sometimes called place-value notation) is a method of encoding numbers. It differs from other notations (such as Roman numerals) in that it uses the same symbol for different orders of magnitude depending on its position. For example, consider the number 23. The “3” indicates 3 ones, because it is in the ones position. The “2”, however, indicates 2 tens, because it is in the tens position. We know the value of a position by its location within the number. As we move left in a number, each position is valued at ten times the prior position. It might help if we label each position using power notation. Consider the number 123:

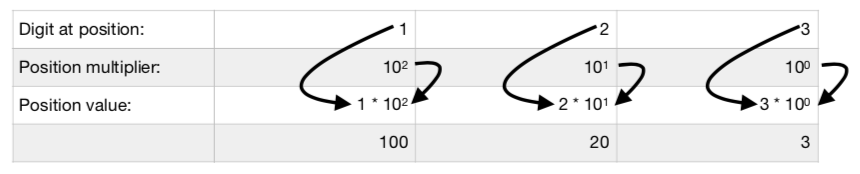
The “3” is the right-most, and therefore the lowest-valued position, representing “ones” with a position multiplier of 100 (that is, 10 raised to the zero power, or 1). The “2” is located one position to the left, so we multiply by 10 again giving us a position multiplier of 101 (that is, 10 raised to the first power, or 10). Finally, the “1” is located one position to the left, so we again multiply by 10 giving us a position multiplier of 102 (that is, 10 raised to the second power, or 100). By multiplying each digit by its corresponding position multiplier, we can obtain the value of the entire number:

1 * 10² + 2 * 10¹ + 3 * 10⁰ =
100 + 20 + 3 =
123

While we generally understand the mechanics of this process in the decimal system, thinking about how it actually works will enable us to consider other systems.

Number Base

The radix or base is the number of unique digits, including zero, used to represent numbers in a positional numeral system. The base is normally written as a subscript to the right of the number. For example, the decimal number 123 would formally be written as (123)₁₀
Note that the parentheses are sometimes not written: 123₁₀
In the case of decimal (base 10) numbers, the subscripted 10 is often assumed and not written.

Decimal System

The decimal system is the system with which we are most familiar. It is a decimal system because it contains ten unique digits:

0 1 2 3 4 5 6 7 8 9

For any (integer) value larger than 9, we’re required to use positional notation. Please keep in mind that “10” is not a digit. Rather, it’s a number consisting of two digits, a “1” in the tens (10¹) position and a “0” in the ones position (10⁰).

Octal System

The octal system uses eight unique digits to represent a number:

0 1 2 3 4 5 6 7

Let’s consider the value of an octal number: 4735₈

What is the decimal value of this number? We use exactly the same method that we use for knowing the value in any system:

Digit at position:	4	7	3	5
Position multiplier:	83	82	81	80
Position value:	4 • 83	7 • 82	3 • 81	5 • 80
	2048	448	24	5

Note that in this case, the right-most digit is, as always, representative of units (ones), just as in any positional system. However, moving one digit to the left, because we’re now using an octal system, the position indicates the number of eights (not tens). The next position to the left indicates the number of sixty-fours (not hundreds) and the final position indicates the number of 512’s. As before, we multiply each digit by its corresponding position multiplier to obtain the value of the entire number:

4 • 8³ + 7 • 8² + 3 • 8¹ + 5 • 8⁰ =
2,048₁₀ + 448₁₀ + 24₁₀ + 5₁₀ =
2,525₁₀

Hexadecimal System

The hexadecimal (six and ten) uses sixteen digits to represent a number:

0 1 2 3 4 5 6 7 8 9 A B C D E F

Note that because we only have ten digits in our familiar decimal system, we use the letters A through F to represent the additional six digits in the hexadecimal system. Remember that these are digits, that is, A represents 10, B represents 11, and so on up to F which represents 15.

Let’s consider the value of a hexadecimal number: B59C₁₆

What is the decimal value of this number?

Digit at position:	B	5	9	C
Position multiplier:	163	162	161	160
Position value:	B • 163	5 • 162	9 • 161	C • 160
	45,056	1280	144	12

As always, we multiply each digit by its corresponding position multiplier to obtain the value of the entire number:

B • 16³ + 5 • 16² + 9 • 16¹ + C • 16⁰ =
45,056₁₀ + 1280₁₀ + 144₁₀ + 12₁₀ =
46,492₁₀

Binary System

The binary system (two) uses two digits to represent a number:

0 1

Let’s consider the value of a binary number: 1011 1010₂
What is the decimal value of this number?

Digit at position:	1	0	1	1	1	0	1	0
Position multiplier:	27	26	25	24	23	22	21	20
Position value:	1 • 27	0 • 26	1 • 25	1 • 24	1 • 23	0 • 22	1 • 21	0 • 20
	128	0	32	16	8	0	2	0

Multiplying each digit by its corresponding position multiplier to obtain the value of the entire number:

1 • 2⁷ + 0 • 2⁶ + 1 • 2⁵ + 1 • 2⁴ + 1 • 2³ + 0 • 2² + 1 • 2¹ + 0 • 2⁰ =
128₁₀ + 0₁₀ + 32₁₀ + 16₁₀ + 8₁₀ + 0₁₀ + 2₁₀ + 0₁₀ =
186₁₀

Formal Representation

Let x be a string of digits, such that: $x=x_{n}x_{n-1}x_{n-2}\cdots x_{0}$

Then, the value of $x$ in any particular base, $b$, is calculated as: $\sum _{i=0}^{n}x_{i}\cdot b^{i}$

The rightmost digit, $x_{0}$ is referred to as the least significant digit, or LSD. It is least significant because in terms of the overall value of the entire number, this digit will always have the least impact. Conversely, the leftmost digit, $x_{n}$ is referred to as the most significant digit, or MSD. It is most significant because in terms of the overall value of the entire number, this digit will always have the most impact.

Converting from Decimal to Another Base

To convert a decimal (base 10) number to any other base, we simply repeatedly divide by the base until we have a quotient of zero. Specifically, the dividend starts with the number that we want to convert, the divisor will always be the base. The remainder of each successive operation indicates the digit in the new base first at the right-most position and then moving left. The quotient of each step becomes the dividend of the subsequent step.

Let’s first try converting the number 28₁₀ to octal (base 8):

The dividend is the decimal number that we want to convert, in this case 28. The divisor is the base to which we want to convert, in this case 8. The remainder indicates each successive digit. We stop the process when the quotient is 0.

Step	Dividend	Divisor	Quotient	Remainder
1	28	8	3	4
2	3	8	0	3

So, 28₁₀ is 34₈. (Remember that we read the remainder from bottom to top.)

Let’s try converting the number 567₁₀ to octal:

Step	Dividend	Divisor	Quotient	Remainder
1	567	8	70	7
2	70	8	8	6
3	8	8	1	0
4	1	8	0	1

So, 567₁₀ is 1067₈.

Let’s try converting the number 63,215₁₀ to hexadecimal:

Step	Dividend	Divisor	Quotient	Remainder
1	63215	16	3950	15
2	3950	16	246	14
3	246	16	15	6
4	15	16	0	15

So, 63,215₁₀ is hexadecimal [15][6][14][15], or more conventionally, F6EF₁₆.
(Remembering that in hexadecimal, we use the digit “F” for 15, “E” for 14, etc.)


Finally, let’s convert the number 53410 to binary:

Step	Dividend	Divisor	Quotient	Remainder
1	534	2	267	0
2	267	2	133	1
3	133	2	66	1
4	66	2	33	0
5	33	2	16	1
6	16	2	8	0
7	8	2	4	0
8	4	2	2	0
9	2	2	1	0
10	1	2	0	1

So, 534₁₀ is 10 0001 0110₂

Customs

• It is customary to separate groups of three decimal digits by commas. For example: 123,456₁₀.
• It is customary to separate groups to two hexadecimal digits by spaces and prefix a leading zero to what would otherwise be a single digit. For example: 01 2F₁₆.
• It is customary to separate groups of three octal digits by spaces and prefix leading zeros to pad to a three digit grouping. For example: 001 237₈.
• It is customary to separate groups of four binary digits by spaces and prefix leading zeroes to pad to a four digit grouping. For example: 0001 1011 1100₂.

Shortcut Conversions

	Coming Soon
	Conversions from/to binary, octal, and hexadecimal

References

• Positional Notation (Wikipedia)
• Radix (Wikipedia)