W3152 Binary Trees
Prerequisites[edit]
Introduction[edit]
Binary Trees are a specific version of the General Tree. They're used to represent hierarchical data and can provide very fast operations such as insertion, deletion, searching, etc. The difference between the General Tree and a Binary Tree is that a Node in a Binary Tree can have 0, 1, or 2 Child Nodes. Its limit of having only 2 child Nodes is why it's called a Binary Tree.
In this lesson, you'll learn the structure of a Binary Tree, learn how to implement it in Swift, and how to perform several essential operations on a Binary Tree. You'll also learn about an offshoot of Binary Trees called the Binary Search Tree, which provides further efficiencies.
Structure[edit]
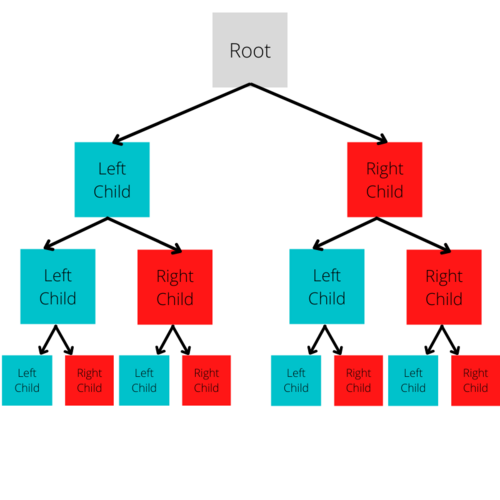
First, let's start by explaining the structure of a Binary Tree. As a refresher, the top level of a Tree is called Level 0. The Node at this level is called The Root. This is where the Tree starts. Now, recall that every Node can have a value, and it can reference other Nodes called Child Nodes. In a Binary Tree, the number of Child Nodes is limited to 2, and these are called the Left Child and Right Child.
Putting this all together, this means that the structure of a Binary Tree starts at the Root, which contains some value and can reference at most, 2 other Nodes. Each of these Nodes can have its own value and can reference 2 more Nodes. This is repeated until all the Nodes in all the branches of the tree end with Leaves, which are simply Nodes that do not have any Child Nodes.
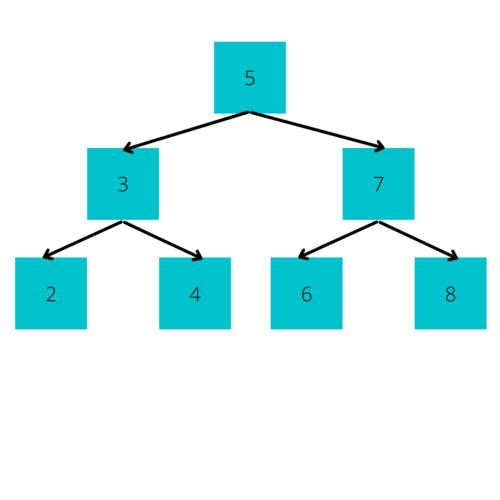
Another version of these is the Binary Search Tree. These Trees are of the exact same structure except for one key difference. In a Binary Search Tree, the Left Node always contains a value less than its parent Node, and the Right Node always contains a value greater than or equal to its parent Node.
We will discuss these more later when we cover how to implement Binary Search Trees with Swift.
Usages[edit]
Binary Trees are used in some capacity in nearly every computer system. Binary Trees are typically changed into more complex, specific trees such as Binary-Search Trees, AVL Trees, Red Black Trees, and others. Binary Search Trees, for example, are very commonly used in searching applications where data is coming in and leaving quickly, Syntax Trees are used in compilers, Heaps are used in path-finding algorithms, etc.
In truth, the more complex data structures you understand, the more difficult they become to distinguish with other data structures and their applications. It's more important to understand that Binary Trees and their varieties are designed as a logical way of storing data. A fun example is Morse Code, which logically works using a Binary Tree.
Complexities[edit]
Now, before going into the Swift implementation, let's touch on the Time and Space Complexities of Binary Search Trees. It is essentially just the sorted version of a Binary Tree and provides more efficient times to perform operations. In terms of Time Complexities, Binary Search Trees provide a logarithmic time complexity for searching, inserting, and deleting while having linear space complexity.
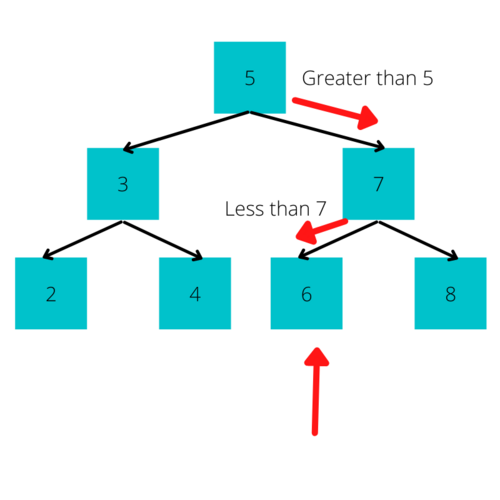
Searching through Binary Search Trees is very similar to how Binary Searches themselves work. If you wanted to insert a Node with the value 5 to the above Binary Search Tree, you would simply do the following:
- Look to see if the current Node is empty. If it is, put the value there.
- If it wasn't empty, see if your value (in this case 5) is greater than or less than the value in the current Node.
- If your value is greater, go to the Right Child; if it's less, go to the Left Child
This operation continues until it finds an empty Node and works almost identically to the famous Binary Search algorithm. This is why the time complexities are so efficient for this data structure and why Search Engines use the data structure so often.
Quiz[edit]
Swift Implementation[edit]
Now, let's get into a basic implementation and then dive into how we can perform some relatively complex algorithms using Binary Trees. As always, we'll start by making a class for our Nodes. Here, we'll give each node a variable for its value and then a leftChild and rightChild. Of course, not every Node will have a Child, so we'll keep those variables optional. However, every Node must have a value, so we'll set it during the init.
class Node<T>{
var value: T
var leftChild: Node?
var rightChild: Node?
init(value: T){
self.value = value
}
}
Additionally, we're using Generics so we won't be restricted to one data type. Now, we technically have everything we need for a Binary Tree; however, we'll also throw in the following function that allows us to give any Node its child elements.
func addChild(leftChild: Node?, rightChild: Node?){
self.leftChild = leftChild
self.rightChild = rightChild
}
Now, we need to provide a way to see our Tree when we print it. This lets us verify that our code is working. After that, we can test the methods. To do that, we'll use an Extension for a Custom String Convertible, similar to past data structures.
extension Node: CustomStringConvertible {
var description: String {
return "\(value)" + " {" + "\(leftChild as Optional)" + ", " + "\(rightChild as Optional)" + "} "
}
}
Now, let's test our tree with some basic numbers, then we can print out the binary tree.
var a = Node(value: 1)
var b = Node(value: 2)
var c = Node(value: 3)
var d = Node(value: 4)
var e = Node(value: 5)
a.addChild(leftChild: b, rightChild: c)
b.addChild(leftChild: d, rightChild: e)
//will print the following: 1 {Optional(2 {Optional(4 {nil, nil} ), Optional(5 {nil, nil} )} ), Optional(3 {nil, nil} )}
//or more simply: 1 {2, {4, 5}, 3, {}}
This works as a quick and simple way of making a Binary Tree. Now, let's add some of the more complex search, traversal, and insertion functions. First, we'll start by upgrading our insertion function to keep the Tree always sorted as a Binary Search Tree. Also, let's rename the class from Node to BinaryTree to represent the new logic.
func insert(value: T){
if value < self.value {
if let left = leftChild {
left.insert(value: value)
} else {
leftChild = BinaryTree(value: value)
}
} else {
if let right = rightChild {
right.insert(value: value)
} else {
rightChild = BinaryTree(value: value)
}
}
}
This goes through the same logic outlined for a Binary Search Tree earlier. It looks at the current Node, and if it's empty it inserts the value there. Otherwise, it moves to either the left or the right Node depending on if its value is greater or less than the current Node. Now, we can now try out our new binary tree by using the insert function.
var a = BinaryTree(value: 1)
a.insert(value:3)
a.insert(value:0)
a.insert(value:2)
If you run this code yourself, you can see it's working as expected, and the numbers are ordered smallest to largest, left to right. Next, we'll add a function for searching through the Binary Search Tree. This process is essentially the same as the function for insertion, except we'll be returning only the node that matches the target value.
public func search(value: T) -> BinaryTree? {
var node: BinaryTree? = self
while let n = node {
if value < n.value {
node = n.leftChild
} else if value > n.value {
node = n.rightChild
} else {
return node
}
}
return nil
}
}
Finally, let's try adding some functions for traversal. We can use three ways to traverse a Binary Tree: Pre-order, Post-order, and In-order. We'll look at how to implement each of these with our examples.
Let's start with In-order traversal. The idea of In-order traversal is to quite simply traverse through the left side of a Binary Tree, then we look at the root, and then we traverse through the right side of the Binary Tree. This operation can be done very easily with recursion.
public func traverseInOrder(process: (T) -> Void) {
leftChild?.traverseInOrder(process: process)
process(value)
rightChild?.traverseInOrder(process: process)
}
}
To test this function, use the code below. All that's happening is we're traversing through the Tree in the same way we did during the binary search and then taking that value and putting it into the print statement. That print statement then prints whatever arguments it gets from the function.
a.traverseInOrder { print($0) }
The other methods of traversal are fairly similar. Pre-order traversal simply has us visiting the Root first, followed by traversing through the Left side of the Binary Tree, and then the Right side. In contrast, with Post-order traversal, we look at the Left side of the Tree, then the Right side, and finally we visit the root. The code for both of these functions is below.
public func traversePreOrder(process: (T) -> Void) {
process(value)
leftChild?.traversePreOrder(process: process)
rightChild?.traversePreOrder(process: process)
}
public func traversePostOrder(process: (T) -> Void) {
leftChild?.traversePostOrder(process: process)
rightChild?.traversePostOrder(process: process)
process(value)
}
As you can see, these methods are almost entirely the same, but think about what effect the changing order has on traversing the Tree. Why might you use one method over the other?
Key Concepts[edit]
- Binary Trees are identical to General Trees, except they have up to 2 Children only
- Binary Trees can have a Left Child and a Right Child
- Binary Search Trees are such that the Left Child is less in value than the Parent, and the Right Child is greater in value than the Parent
- Binary Search Trees are often used for their consistently fast times to perform operations
Exercises[edit]
- Analyze the different ways of traversing through a Binary Tree, see what effect this has on the order of the Nodes visited
- Try to make a function that can fill a Binary Search Tree of Integers with an array of Integers as the argument
- See what other ways you can make a Binary Tree using the features of Swift and try other implementations, analyze what effect, if any, this has on the end structure