W2222 Recursion

Within these castle walls be forged Mavens of Computer Science ...

— Merlin, The Coder

Visual Recursion

Background[edit]

Recursion (Wikipedia)
Factorial (Wikipedia) Read up to the section "Number Theory," exclusive
Fibonacci Number (Wikipedia) Read up to the section "Mathematics," exclusive
What on Earth is Recursion? (YouTube - Computerphile)

Introduction[edit]

Recursion is a very common topic in computer science. It can also be one of the most difficult to understand. The basic premise of recursion is using a function that executes over and over again until some base condition is met and the problem is solvable. Many forms of sorts, traversals, and searches rely on using recursive functions, and it is a concept you should be familiar with.

Concept of Recursion[edit]

The idea behind recursion is that the function breaks up a problem into several smaller problems that can be more easily solved. Therefore, a recursive function calls itself until the problem is easy enough to solve, and the multiple small solutions can be used together to solve the larger problem.

Most recursive functions have essentially two sections: the base case and the recursive step. The recursive step is one in which the function calls itself again, often with some modified data. The base case is one in which a developer tells the program what is a small enough problem that can be solved immediately. It is the point at which the function no longer needs to break down the problem.

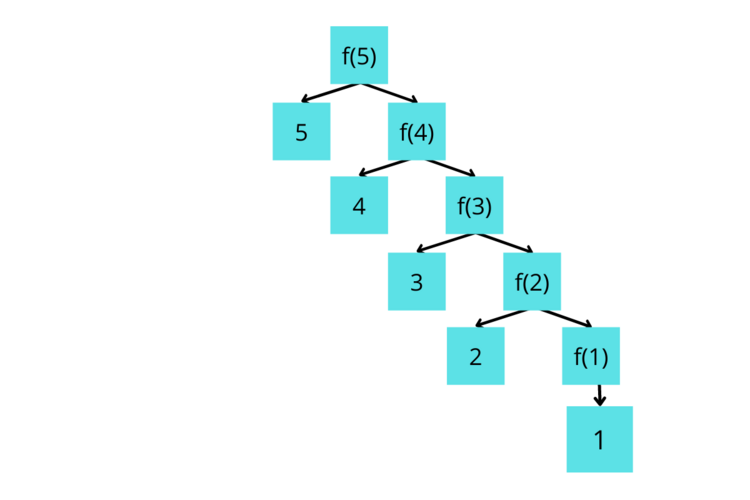
Let's look at this with a simple Recursive function. All we'll do is make a function called printReverse. This returns a string that counts down from a number, so the function call countDown(5) returns "5 4 3 2 1". Note that this function can also be implemented with iteration; although, recursion should generally not be seen as a counterpart to iteration because they function differently. For the sake of demonstration, we'll start here and later move onto more recursive-specific examples.

func countDown(from target: Int) -> String {
     if(target == 1) {
         return "1"
     } else {
         let string = String(target)
         return string + " " + countDown(from: target - 1)
     }
}

print(countDown(from: 5))

Notice the base case. We state that if our number is 1, we can simply return that number and essentially tell the recursive function to stop calling itself.

Let's walk through the function step by step. We've been given the integer 5. This does not equal 1, so we move to the "else" block. We make a string "5" and return this with a recursive call with the parameter 4. The same process occurs, and we return "4" as a string. Then we call the function again with the parameter 3. This keeps happening until we get 1, and we simply return 1, thus having returned 5 4 3 2 1.

If you're still confused, see the image below or try breaking the function down yourself with pen and paper.

A function that uses recursion to return 5 4 3 2 1.

Keep in mind that with recursive functions, it is very easy to accidentally cause the function to keep calling itself infinitely. The base case must be one that is attained by whatever logic the recursive step is using. This is a great area for using preconditions.

Quiz[edit]

Usages[edit]

Recursive functions are used in several ways. The ability to break down a problem into smaller steps can provide some very quick algorithms and patterns of solving a problem. Below, we'll go through two of the most famous applications of Recursion.

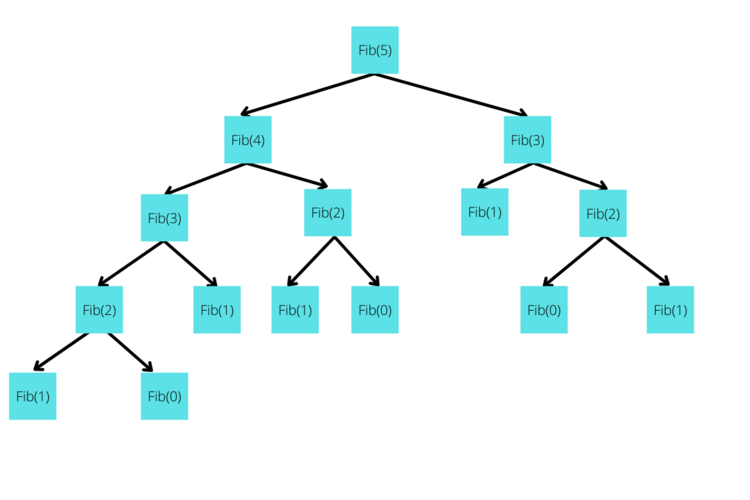
To begin, let's tackle the print Fibonacci. Essentially, the goal is to print the Fibonacci number at the parameter n. The Fibonacci numbers are simply 1, 1, 2, 3, 5, 8, 13, etc., where the next number is the sum of the prior two. Therefore, the call fib(5) returns 8, fib(6) returns 13, and so on. To do this, you'll need to do some more complex logic before the recursive step. Try solving this on your own first and then look at the solution.

func fib(int: Int) -> Int {
  if(int <= 1){
    return 1
  }
  else{
    return fib(int: int-1) + fib(int: int-2)
  }
}

This might have taken you a while, but it's pretty simple when you understand the Base Case. All we have to do is call the function again twice in the recursive step. This gets the two fib numbers that came before the number you are looking for. By adding these two numbers, you then have the desired number. And because the 0th number in the Fibonacci sequence is 1, we'll want to make sure our base case reflects this.

For sizing purposes, the above shows the call to fib(5)

For the call fib(6), we call fib(5) and fib(4) and add these two together. fib(5) and fib(4) eventually is evaluated as 8 and 5, but first they'll be broken into fib(4) + fib(3), and fib(3) + fib(2). Eventually, this entire call is broken down into fib(1) + fib(1) + fib(0) + fib(1) + fib(0) + fib(1) + fib(1) + fib(0) + fib(1) + fib(1) + fib(0) + fib(1) + fib(0). This can all be evaluated by our base case into 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1, which equals 13.

This should give you an idea of how recursion works. Simply making the problem smaller and easier to solve, and, in this case, breaking it down into simple 1 + 1.

This recursive methodology is used in several algorithms such as Tree Traversing, Merge Sorting, and Complex Computations. Often, these require less code and take much less time to perform the operations.

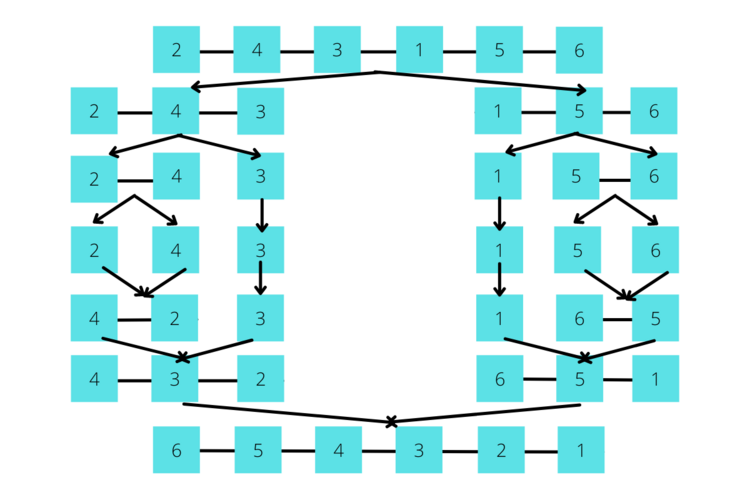
Let's take a look at the Merge Sort to see how it uses Recursion to sort arrays incredibly quickly. Although we won't be implementing the code for this, it's good to take a look at the conceptual use of Recursion.

If you're unfamiliar, a Merge Sort operates by breaking up an array into smaller and smaller arrays and then merging them back together in the correct order. This is the exact methodology of Recursion.

A visual representation of merge sort

The Merge Sort has two functions: MergeSort() and Merge(). The MergeSort() breaks up the array into arrays of length 1 (the base case). Then the Merge Function takes the pieces made by the Merge Sort and stitches them together as sorted. This allows for significant time optimizations, which is why it is one of the quickest forms of the many sorting algorithms.

It's clear to see that Recursion's methodology of breaking up a problem into several smaller problems can be very useful in an application. Think of the areas where you can apply this methodology and how it might contrast from other algorithms.

Quiz[edit]

Key Concepts[edit]

Key Concepts

The main concept of Recursion is to take a problem and break it down until it can be easily solved
The Base Case is the point at which the problem can be easily solved
The Recursive Step is where the function calls itself, often with a different parameter or different logic
Infinite Recursion should be avoided by making sure the Base Case and Recursive Step work so there is an end to the breaking down of the problem

Exercises[edit]

Exercises

M2222-10 Complete Merlin Mission Manager Mission M2222-10.

	To break down a problem through a series of iterations
	To call a function over and over in hopes that it solves the problem
	To break down a problem into simpler problems that can be easily solved
	To break down a problem into a series of steps that can be followed to solve the problem

	It is where the function calls itself again
	It is where some logic is performed to accomplish the given task
	It is the point at which the program enters infinite recursion
	It is where the function stops calling itself because the problem has been broken down enough

	It is used for storing data in a hierarchy
	It is used for storing data to show relationships between the data
	It is used for used in search applications where insertion and deletion is common
	It is used for used to store data linearly

	True
	False

	True
	False

	True
	False

	True
	False