W1032 Negative Integers
Prerequisites[edit]
Encoding Options[edit]
Reserved Bit[edit]
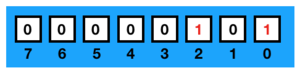
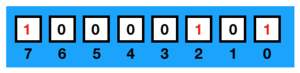
What methods might we use to encode negative integers? As a first approach, perhaps we can use one of the bits of our word to represent the sign. Let's consider a single-byte word and the number . This may be encoded as:
If we were to reserve the most-significant bit, bit seven, to indicate whether our number was positive or negative, we can use the remaining seven bits to store the absolute value of the number. In such a case, the number would be encoded as:
Initially this may appear to be a good solution, but let's explore further.
Reserved Bit Encoding
- How would be encoded?
- How would be encoded?
- How would you add these two numbers () in binary?
- How many alternative representations are there for the number 0?
- Given the above, do you think that this method of encoding is ideal? Why or why not?
Let's consider what our goals should be for an ideal encoding scheme.
- We shouldn't waste bit patterns (in other words, each bit pattern should identify a unique number)
- We should easily be able to add positive numbers to one another
- We should easily be able to add negative numbers to one another
- We should easily be able to add numbers of opposite sign
Complements[edit]
A complement is something that is required to complete a whole. Colors have complements, shapes have complements, and numbers have complements. In the following sections we'll investigate some common numerical complements.
Nines' Complement[edit]
Consider the aforementioned goals; are we able to meet them? Consider the decimal number system and a need to subtract two numbers. (Remember that when subtracting M - S we refer to M as the minuend and S as the subtrahend.) Let's subtract 7 - 3 to obtain 4. Is there another method that we can use to obtain the same result? We can use nine's complement by subtracting each digit of the subtrahend from 9. In this case, we'll have 9 - 3, or 6. If we then add this to our original minuend, 7, we'll have 7 + 6 = 13. But wait! That's not four. However, if we drop the carry and add one we'll have 4.
Let's try this with some larger numbers, 742 - 359. The result is 383. The nine's complement of the subtrahend is 9-3=6, 9-5=4, and 9-9=0, yielding 640.
 Helpful Hint
Helpful Hint
A shortcut to obtaining nine's complement is simply to use the same number of 9's as are present in the subtrahend to form a minuend and then perform the subtraction. In the above example, this would simply be 999 - 359 = 640.
Continuing, we'll add this number to our original minuend, 742, and obtain 742 + 640 = 1,382. Dropping the carry and adding one we'll have 383, the desired result. For decimal numbers, the algorithm is therefore:
- Take the nine's complement of the subtrahend
- Add this number to the original minuend
- Drop the carry
- Add one
Tens' Complement[edit]
We can simplify this a bit by adding the one when calculating the complement of the subtrahend. For the decimal number system, this would be called the ten's complement. Our improved algorithm is therefore:
- Take the ten's complement of the subtrahend
- Add this number to the original minuend
- Drop the carry
Let's try it. Given 9,228 - 6,125 = 3,103. Using our algorithm:
- Take the ten's complement of the subtrahend -> 9,999 - 6,125 = 3,874 -> 3,874 + 1 = 3,875
- Add this number to the original minuend -> 9,228 + 3,875 = 13,103
- Drop the carry -> 13,103 without carry = 3,103 ✓
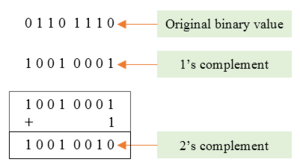
Ones' Complement[edit]
This same method can be used for binary numbers, but in the case of binary numbers, it's even easier! The complement of 0 is 1 while the complement of 1 is 0.
Twos' Complement[edit]
As in the case of tens' complement, twos' complement can be obtained by adding one to one's complement.
| Coming Soon | |
|
Exercises[edit]
- M1032-10 Complete Merlin Mission Manager Mission M1032-10.
References[edit]
- Complements (Wikipedia)