Curriculum[edit]
| Coder Merlin™ Computer Science Curriculum Data | |
|
Unit: Boolean algebra Experience Name: Binary Adders (W1017) Next Experience: () Knowledge and skills:
Topic areas: Boolean algebra Classroom time (average): 30 minutes Study time (average): 60 minutes Successful completion requires knowledge: understand the construction and use of binary adders Successful completion requires skills: demonstrate proficiency in constructing and using binary adders |
Introduction[edit]
One of the most fundamental operations performed by computers, aside from the logical operations that we've already discussed, is the arithmetic operation of addition.
Half-Adder[edit]
Let's consider what's required to add two, single-bit binary integers. We'll need one bit to represent the sum of the integers, and another to handle the carry. Representing this in the form of a truth table yields:
| Inputs | Outputs | ||
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
This is formally termed a half-adder, a logic circuit capable of adding two bits.
- What truth table do you recognize that produces the output of the Carry column?
- What truth table do you recognize that produces the output of the Sum column?
Full-Adder[edit]
In order to add two single-bit binary integers PLUS a carry, we need an adder capable of adding three single-bit binary numbers. Again, we'll need one bit to represent the sum of the integers, and another to handle the carry. Representing this in the form of a truth table yields:
| Inputs | Outputs | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
This is formally termed a full-adder, a logic circuit capable of adding three bits.
- What do you notice about the relationship between the first-half (top four rows) of the full-adder as compared to all of the rows of the half-adder?
- Why is this true?
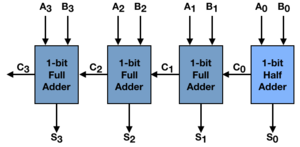
Ripple Carry Adder[edit]
We've learned that a half-adder can add two bits and full-adder can add three bits. How can we add a multi-bit number such as a 16-bit word? By cascading four adders such that the carry output of the prior adder feeds the carry input of the subsequent adder we can add two four-bit numbers. This concept can be easily extended to an arbitrary number of bits.
- Why does the least significant bit position use a half-adder rather than a full-adder?
- Assume that proper inputs are applied for all bits in numbers A and B. Will the correct output from S be available instantaneously? If not, why not?
- Assume that we have a standard (non-scientific calculator) capable of adding two 16-bit words. Two numbers, A and B, are added together. After the addition, it is noted that is high. What can we infer? What is this state commonly called?
Key Concepts[edit]
- A half-adder is a logic circuit capable of adding two bits and output a carry bit and a sum bit.
- A full-adder is a logic circuit capable of adding three bits and output a carry bit and a sum bit.
- A ripple-carry-adder is a logic circuit constructed of adders, cascaded in such a manner that the carry output of each adder feeds the carry input of the subsequent adder. Using this method we are able to add an arbitrary number of bits.
Exercises[edit]
- J1017 Create a journal and answer all questions in this experience. Be sure to:
- edit your journal using emacs within your ~/Journals directory
- properly name your journal as J1017.txt
- include all sections of the journal, properly formatted
- push your changes to GitHub
- properly tag your journal as J1017.Final
- push your tag to GitHub
- Construct your work using Falstad's Editor
- All circuits must be on a single page
- Label the page (using Text) with:
- Your name
- The date
- Begin each circuit with a Blank Circuit
- Label each circuit diagram (using Text) with:
- The name of the logic gate (e.g. "NOT")
- Each output (e.g. "sum", "carry out")
- Save the document using the
Save As...option from the File submenu and then click on the link presented - The file contains your work for the exercise. Create a new subdirectory, J1017, in your Journals directory. Upload the file to the J1017 directory via SFTP. Be sure to push the files to your GitHub repository.
- You may use any of the following logic gates in your implementation: AND, OR, NOT, XOR, NAND, and NOR
- Construct a half-adder
- Construct a full-adder
- M1017-31 Complete Merlin Mission Manager Mission M1017-31.
References[edit]
- Adder (Wikipedia)
- Schocken, Simon and Nisan, Noam. The Elements of Computing Systems. MIT Press, 2005.
Experience Metadata
| Experience ID | W1017 |
|---|---|
| Next experience ID | |
| Unit | Boolean algebra |
| Knowledge and skills | §10.331 |
| Topic areas | Boolean algebra |
| Classroom time | 30 minutes |
| Study time | 1 hour60 minutes <br /> |
| Acquired knowledge | understand the construction and use of binary adders |
| Acquired skill | demonstrate proficiency in constructing and using binary adders |
| Additional categories |