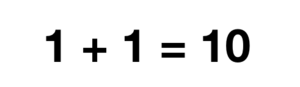Curriculum[edit]
| Coder Merlin™ Computer Science Curriculum Data | |
|
Unit: Numbers Experience Name: Alternative Base Addition (W1012) Next Experience: () Knowledge and skills:
Topic areas: Positional notation Classroom time (average): 60 minutes Study time (average): 180 minutes Successful completion requires knowledge: understand positional notation; understand how numbers specified in positional notation are added Successful completion requires skills: ability to use positional notation to represent numbers in the binary, octal, decimal, and hexadecimal systems; ability to convert between representations of numbers in the binary, octal, decimal, and hexadecimal systems; ability to count by one using numbers in the binary, octal, decimal, and hexadecimal systems; ability to add together numbers in the binary, octal, decimal, and hexadecimal systems |
Addition (Decimal System)[edit]
Addition is a basic (and critical) operation. Important properties of addition include:
- Addition is commutative, meaning that the order of the operands does not matter
- Addition is associative, meaning that when we're adding more than two operands, the order that we perform the addition does not matter
- The identity element for addition, also termed the additive identity, is zero
- The operator for addition is the plus () sign
- The operands for addition are called addends
Let's review how we perform addition in the number system with which we are most familiar, the decimal system.
There are a few simple rules when adding non-negative, whole numbers:
- Align the addends vertically, flush right. (This step ensures that the position multiplier is the same for both addends in each column.)
- If any addend has fewer digits than the addend with the maximum digits, we may place a zero in columns to the left of the existing addend. (Leading zeroes don't affect the value.)
- Starting from the right-most column, add the two digits of the addend and the carry. Note that this means that we are adding three operands in each column. If the sum exceeds the quantity that can be represented with a single digit, carry a one to the column to the left.
- Repeat the process with the column to the left until reaching the final column.
Let's look at a few examples:
[edit]
To add we:
|
|
[edit]
To add we:
|
|
[edit]
To add we:
|
|
- Describe the general process for executing addition, regardless of base.
Addition (Octal System)[edit]
There's no need for any additional rules for the octal system. In fact, for all systems, the rules are exactly the same! But let's review the octal number line before proceeding to an example:

How would we add ?

Be sure that you fully understand the above diagram before proceeding.
[edit]
To add we:
|
|
- What special factors need to be considered when executing addition with octal numbers?
Addition (Hexadecimal System)[edit]
Let's review the hexadecimal number line before proceeding to an example. How would we add ?

Remember that in number systems with bases greater than 10, by convention, we use letters in place of digits.
| Digit | Value |
|---|---|
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
[edit]
To add we:
|
|
- What special factors need to be considered when executing addition with hexadecimal numbers?
Addition (Binary System)[edit]
Let's jump right in to an example:
[edit]
To add we:
|
|
- What special factors need to be considered when executing addition with binary numbers?
Key Concepts[edit]
- Addition is a basic (and critical) operation
- Addition is commutative
- Addition is associative
- The identity element for addition, also termed the additive identity, is zero
- The operator for addition is the "+" sign
- The operands for addition are called addends
- When adding non-negative, whole numbers:
- Align the addends vertically, flush right
- If any addend has fewer digits than the addend with the maximum digits, we may place a zero in columns to the left of the existing addend
- Starting from the right-most column, add the two digits of the addend and the carry. If the sum exceeds the quantity that can be represented with a single digit, carry a one to the column to the left.
- Repeat the process with the column to the left until reaching the final column
Exercises[edit]
- J1012 Create a journal and answer all questions in this experience. Be sure to:
- edit your journal using emacs within your ~/Journals directory
- properly name your journal as J1012.txt
- include all sections of the journal, properly formatted
- push your changes to GitHub
- properly tag your journal as J1012.Final
- push your tag to GitHub
- M1012-10 Complete Merlin Mission Manager Mission M1012-10.
References[edit]
- Addition (Wikipedia)
Experience Metadata
| Experience ID | W1012 |
|---|---|
| Next experience ID | |
| Unit | Numbers |
| Knowledge and skills | §10.311 §10.312 §10.313 |
| Topic areas | Positional notation |
| Classroom time | 60 minutes |
| Study time | 3 hours180 minutes <br /> |
| Acquired knowledge | understand positional notation understand how numbers specified in positional notation are added |
| Acquired skill | ability to use positional notation to represent numbers in the binary, octal, decimal, and hexadecimal systems ability to convert between representations of numbers in the binary, octal, decimal, and hexadecimal systems ability to count by one using numbers in the binary, octal, decimal, and hexadecimal systems ability to add together numbers in the binary, octal, decimal, and hexadecimal systems |
| Additional categories |