User:William-chin
Background[edit]
- Read Quick Sort Algorithm (Wikipedia)
- View Quick Sort Algorithm (YouTube)
- View Quick Sort Algorithm (YouTube)
Introduction[edit]
The quicksort algorithm is generally known as one of the fastest sorting algorithms, many times faster than heap sort. If implemented well, quick sort algorithms can have a complexity of O(n log n)
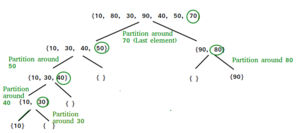
Algorithm[edit]
The quicksort algorithm calls for a pivot during its recursive calls, here is an overview:
- Pick an element as a pivot
- Create 2 markers, which will be compared with a < function in order to set values up for a partition
- Create a partition, which will be used to put elements in an array smaller than x and greater than x
- Repeat steps 2 and 3 until the array is sorted
Implementation[edit]
Quicksort algorithms vary, partitions and pivot elements can be different for each algorithm. The partition and method of obtaining a pivot element usually depend on what is being sorted, and what level of Big O complexity the algorithm is aiming for.
- First, create a partition
* A partition will take the pivot point(x) and put all smaller elements before x, and all larger elements after x * in order to do this, we will need to keep track of the leftmost and rightmost index with 2 pointers( or markers) * While traversing elements, if we find a smaller element (an element smaller than x), we will swap the lower element to the left * Otherwise, if there aren't any smaller elements, we will ignore the current element
- Then recursive calls of these partitions will be made until the array is sorted
Performance[edit]
As seen before, the average performance of quicksort is O(n log n) complexity, but how quicksort algorithms work, depends on the method of obtaining a pivot point, and how partitions are made (based on how array elements were originally inputted), quicksort can have a worse case complexity of O(n^2).
Exercises[edit]
- M1352-10 Complete Merlin Mission Manager Mission M1352-10.