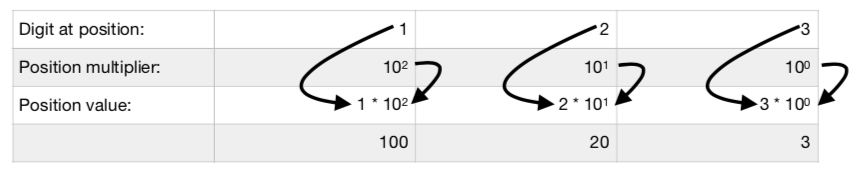
Positional notation (sometimes called place-value notation) is a method of encoding numbers. It differs from other notations (such as Roman numerals) in that it uses the same symbol for different orders of magnitude depending on its position. For example, consider the number 23. The “3” indicates 3 ones, because it is in the ones position. The “2”, however, indicates 2 tens, because it is in the tens position. We know the value of a position by its location within the number. As we move left in a number, each position is valued at ten times the prior position. It might help if we label each position using power notation. Consider the number 123:
The “3” is the right-most, and therefore the lowest-valued position, representing “ones” with a position multiplier of 100 (that is, 10 raised to the zero power, or 1). The “2” is located one position to the left, so we multiply by 10 again giving us a position multiplier of 101 (that is, 10 raised to the first power, or 10). Finally, the “1” is located one position to the left, so we again multiply by 10 giving us a position multiplier of 102 (that is, 10 raised to the second power, or 100). By multiplying each digit by its corresponding position multiplier, we can obtain the value of the entire number:
1 * 102 + 2 * 101 + 3 * 100 =
100 + 20 + 3 =
123
While we generally understand the mechanics of this process in the decimal system, thinking about how it actually works will enable us to consider other systems.